Ingredient Selection Algorithm
- R
Introduction
In Part 1, we used the stringdist & fuzzyjoin packages to clean the cocktails dataset.
With a tidied dataset, we return to the original problem statement:
What ingredients should you buy in order to maximize your mixological palette? Assume your shopping cart holds items.
Assumptions:
We interpret “maximize mixological palette” to strictly mean achieve as much variety as possible. In other words, we won’t assign weight to the drink based on its popularity.1 For this problem, we are trying to maximize the quantity of substantiated recipes.
For the scope of this post, let’s suppose we are interested in whiskey-based cocktails.
whiskey <- cocktails %>%
with_groups(drink,
filter,
any(str_detect(ingredient, "(bourbon|whiskey)")))
unique(whiskey$drink)## [1] "Algonquin" "Allegheny"
## [3] "Artillery Punch" "Boston Sour"
## [5] "Bourbon Sling" "Bourbon Sour"
## [7] "Brandon and Will's Coke Float" "California Lemonade"
## [9] "Classic Old-Fashioned" "Damned if you do"
## [11] "Egg Nog #4" "Frisco Sour"
## [13] "Hot Creamy Bush" "Imperial Fizz"
## [15] "Irish Coffee" "Irish Curdling Cow"
## [17] "Irish Spring" "Jack's Vanilla Coke"
## [19] "Japanese Fizz" "John Collins"
## [21] "Kentucky B And B" "Kentucky Colonel"
## [23] "Manhattan" "Midnight Cowboy"
## [25] "Mississippi Planters Punch" "New York Sour"
## [27] "Old Fashioned" "Owen's Grandmother's Revenge"
## [29] "Sazerac" "Whiskey Sour"Between these drinks, there are 56 ingredients.
## [1] "blended whiskey" "dry vermouth" "pineapple juice"
## [4] "bourbon" "blackberry brandy" "lemon juice"
## [7] "lemon peel" "tea" "rye whiskey"
## [10] "red wine" "rum" "brandy"
## [13] "benedictine" "orange juice" "lemon"
## [16] "powdered sugar" "egg white" "cherry"
## [19] "sugar" "water" "orange"
## [22] "maraschino cherry" "vanilla ice-cream" "coca-cola"
## [25] "lime" "grenadine" "carbonated water"
## [28] "bitters" "whiskey" "hot damn"
## [31] "egg yolk" "nutmeg" "milk"
## [34] "light rum" "vanilla extract" "salt"
## [37] "whipped cream" "irish whiskey" "irish cream"
## [40] "coffee" "vodka" "peach brandy"
## [43] "sweet and sour" "ice" "tennessee whiskey"
## [46] "port" "club soda" "sweet vermouth"
## [49] "angostura bitters" "orange peel" "dark rum"
## [52] "heavy cream" "beer" "lemonade"
## [55] "ricard" "peychaud bitters"It’s feasible that we could acquire all of these items before the dinner party - given ample time + assuming we could locate these items at one store. We simplify these contingencies into one parameter, , the number of items our shopping cart can hold.
For the sake of discussion, let’s suppose . Where do we start?
Bourbon? Lemons? Sugar? These ingredients have a high occurrence rate in the whiskey dataset - therefore, we assume it would be a valuable use of shopping cart space to grab these ingredients.
Table 1: Most common ingredients in whiskey dataset
Great! Now we can print out Table 1 and take it to the store. It’s important to note that regardless of , we always begin our selection from the top of Table 1 and work our way down.
If , we select bourbon, lemon, and sugar. For , we add blended whiskey and powdered sugar.
We define subset performance as the number of substantiated recipes for a given .
Figure 1 illustrates the overall performance for all values of , adhering to the prescribed order in Table 1.
Figure 1: Set selection performance based on occurrence frequency
Utilizing the selection order provided by Table 1, we would actually need to purchase ingredients to fulfill our first recipe: Kentucky B & B, which is comprised of only two ingredients: (1) bourbon & (2) benedictine.
Something isn’t right - why did we need to purchase 7 ingredients to make a Kentucky B & B? This seems like a waste of shopping cart space. Frequency-based ingredient order is clearly not the optimal selection scheme for our problem statement.
Rethinking the approach
We need to develop an algorithm that embodies the constraints of this problem more effectively than the frequency-based method above.
For example, it is possible to select 7 ingredients to fulfill recipes for Kentucky B & B (2), Algonquin (3), and Midnight Cowboy (2). The key observation is that the total amount of ingredients between these drinks sums to 7.
There is an underlying logic here - any 2nd grader could outperform the frequency-based method when presented this problem (though I’m certainly not condoning underage drinking). But how do we translate this underlying logic into an algorithm?
For each , we could try selecting the ingredient that results in fulfillment of or more recipes.
shopping_cart <- character() # we start with an empty shopping cart
choices <- unique(whiskey$ingredient)
n_recipe_fulfilled <- integer()
# for each choice, how many recipes are fulfilled?
for (j in seq_along(choices)) {
n_recipe_fulfilled[j] <- whiskey %>%
with_groups(drink,
filter,
all(ingredient %in% c(choices[j], shopping_cart))) %>%
count(drink) %>%
nrow()
}
choices[n_recipe_fulfilled > 0]## character(0)But there are no drinks comprised of only ingredient! If this routine will not work for , we certainly cannot generalize it for any arbitrary .
We can augment this approach by revisiting the n_recipe_fulfilled vector, which currently displays fulfilled recipes for a given ingredient choice. If this vector consists of all zeroes, then our algorithm reaches a dead end.
## [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [24] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [47] 0 0 0 0 0 0 0 0 0 0Despite the above result consisting of all zeroes, there has to be an optimal choice. We need to increase the level of granularity available to the algorithm at each .
Suppose, again, that : we currently have ingredients, and we need to choose .
For concise display, we sample drinks from whiskey.
Each shaded block in Figure 2 represents an unfulfilled ingredient.
Figure 2: Remaining ingredients in sample
Between these drinks, there are distinct ingredients. For , this implies choices.
Each choice will reduce the count of ingredients (shaded blocks) in some capacity - it may just be one drink, or multiple drinks, that see a decrease in unfulfilled ingredients.
In Figure 3, we have selected sugar - this brings us 1 ingredient closer to fully substantiating multiple drinks.
Figure 3: Drink sample ingredients after sugar removed
We can notate the remaining ingredients in each drink as a vector:
We then proceed to create a vector for all choices - concatenating the results into a matrix, where is the number of choices at the iteration and is the number of drinks.
choices <- unique(whiskey_sample$ingredient)
n_ingredients_remaining <- whiskey_sample %>%
group_by(drink) %>%
summarise(y = list(ingredient), .groups = "drop") %>%
crossing(choice = choices) %>%
rowwise() %>%
mutate(y = length(y[!y %in% choice])) %>%
ungroup() %>%
arrange(choice, drink) %>%
pivot_wider(values_from = y, names_from = drink)
Table 2: n_ingredients_remaining matrix
From here, how do we decide which choice is best?
- Select row with lowest number. But what if the minimum number is repeated across multiple columns? This method is not capable of identifying as the optimal choice.
- Select row with lowest sum. This would incorrectly prioritize over .
- Select row with lowest sum of squares.Although this method is a step in the right direction, it would incorrectly select over
What we need is a transformation function that amplifies values as they approach 0. We accomplish this with an exponential function.
For each , we apply this transformation to each element in the matrix and select the row containing the maximum sum.2
Figure 4 shows how this logic applies to our example, for all values .
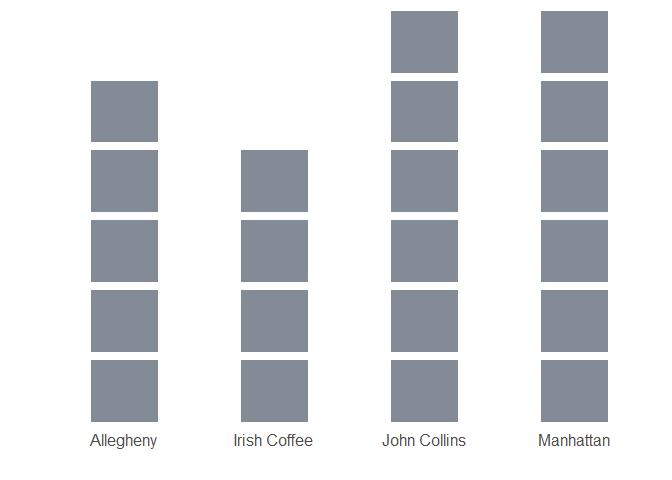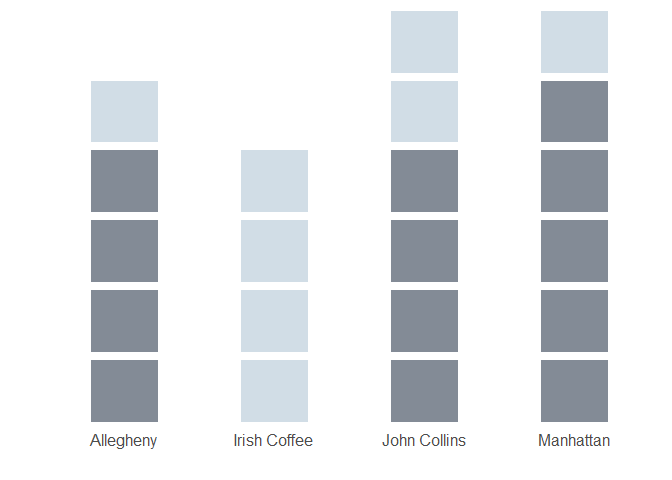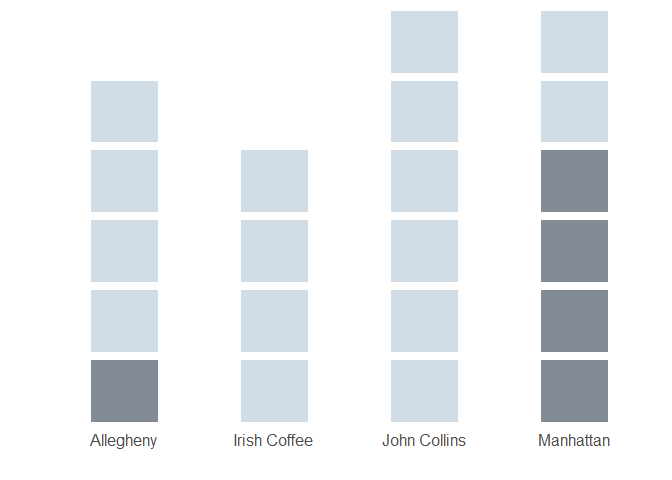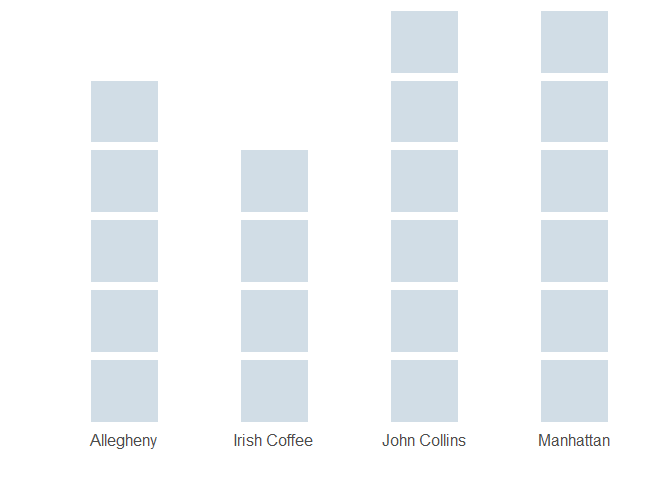
Figure 4: Selection order utilizing remaining-ingredient matrix + transformation fn
I have written a function that performs this algorithm on any dataset sharing a similar structure to cocktails. You can find the implemented form on my Github - this blog post will be updated once I have a chance to create a package for it.
Since the actual form is heavy with rlang syntax, I’ve shown a simplified version below.
# inventory: ingredients already chosen prior to nth iteration
selection_simplified <- function(inventory) {
choices <- setdiff(unique(pull(whiskey, ingredient)), inventory)
a <- whiskey %>%
filter(!ingredient %in% inventory) %>%
group_by(drink) %>%
summarise(y = list(ingredient), .groups = "drop") %>%
crossing(c = choices) %>%
rowwise() %>%
mutate(y = length(y[!y %in% c]),
y = exp(4 / (1 + 5 * y))) %>%
ungroup() %>%
arrange(c, drink)
with(a,
matrix(y,
ncol = n_distinct(c),
dimnames = list(unique(drink), unique(c))
)
) %>%
colSums() %>%
which.max() %>%
names()
}Since the objective at each iteration is exactly the same, the ultimate value of does not impact the optimal selection order, hence we only need to apply selection_simplified to whiskey once.
Mathematically, if we label the output as vector :
out <- character(length = n_distinct(whiskey$ingredient))
for (i in seq_along(out)) {
out[i] <- selection_simplified(out)
}
out # optimized ingredient selection order## [1] "bourbon" "benedictine" "lemon peel"
## [4] "sugar" "water" "lemon juice"
## [7] "angostura bitters" "maraschino cherry" "orange"
## [10] "bitters" "club soda" "dry vermouth"
## [13] "blackberry brandy" "blended whiskey" "pineapple juice"
## [16] "lemon" "lime" "cherry"
## [19] "powdered sugar" "egg white" "red wine"
## [22] "carbonated water" "light rum" "brandy"
## [25] "grenadine" "port" "coca-cola"
## [28] "vanilla ice-cream" "whiskey" "hot damn"
## [31] "dark rum" "heavy cream" "peychaud bitters"
## [34] "ricard" "ice" "vanilla extract"
## [37] "tennessee whiskey" "beer" "lemonade"
## [40] "orange peel" "sweet vermouth" "irish whiskey"
## [43] "coffee" "irish cream" "whipped cream"
## [46] "orange juice" "vodka" "peach brandy"
## [49] "sweet and sour" "rum" "rye whiskey"
## [52] "tea" "egg yolk" "milk"
## [55] "nutmeg" "salt"Results
Figure 5 clearly demonstrates the algorithm outperforms the frequency-based selection scheme discussed in the introduction.
Figure 5: Selection method performance for whiskey dataset
In Figure 6, we we apply these methods to a random sample of drinks from cocktails. Again, the algorithm outperforms the frequency-based method.
Figure 6: Selection method performance for random sample of 20 drinks
We quantify the performance improvement, , by computing the ratio of area under the curves.
The below code takes samples of drinks from
cocktails, calculates the algorithm & frequency-based set order, and computes area under the curve.
The function selection_path is the implemented version of selection_simplified, found on my Github.
capability2 calculates set performance for all values of - we integrate this vector using stats::diffinv to obtain area under performance curve.
cocktail_splits <- list()
set.seed(2020)
for (i in 1:50) {
cocktail_splits[[i]] <- cocktails %>%
filter(drink %in% sample(unique(drink), size = 20))
}
performance_bootstraps <- tibble(cocktail_splits) %>%
mutate(
# calculate set based on algorithm
algorithm = map(.x = cocktail_splits,
.f = selection_path,
ingredient,
drink),
# calculate set based on frequency
frequency = map(cocktail_splits, ~ {
count(..1, ingredient, sort = T) %>%
pull(ingredient)
})
) %>%
mutate(across(c(algorithm, frequency), ~ {
# calculate area under each performance curve
map2_dbl(.x, cocktail_splits, ~ {
capability2(..1, ..2, drink, ingredient) %>%
fill(performance, .direction = "down") %>%
pull(performance) %>%
diffinv(xi = 0) %>%
tail(1)
}
}))) %>%
transmute(id = row_number(),
pa = algorithm / frequency)As shown by the histogram in Figure 7, the algorithm method consistently performs better by at least 44%.
Figure 7: Histogram: Relative performance of algorithmic over frequency-based selection
Finally!
If you’re going shopping for whiskey-based cocktails, Figure 8 is what you want to take with you. This provides an exploded-view of the algorithm-based selection for whiskey. Check out my Shiny app that provides the below grid for numerous subsets of cocktails!
Figure 8: Ingredient grid for whiskey dataset
The method we will end up using for this problem leaves room for assigning weights - I may include this functionality in a package↩︎
In the future, it would be interesting to augment the algorithm to look ahead by several iterations, taking the hypothetical performance of future junctions into consideration. Suppose the 1st-order metric used in this post ranks choices A & B roughly equivalent - does choice A lead to another set of choices that contain a better outcome than those offered by B? What about choices 2 steps after A & B? One could extend this logic to the -order, depending on computational resources.↩︎